Troisième Partie
Modélisation du transport de sédiments autour d'un récif artificiel
*

A/ Le transport par charriage



Introduction
1/Les modèles déterministes
2/Les modèles statistiques
Conclusion

sommaire Troisième Partie

Introduction :

La modélisation du transport solide est un problème loin d'être résolu analytiquement. Les problèmes des écoulements turbulents, majoritairement responsables du transport et de la mise en suspension des particules n'étant pas encore entièrement détaillés, l'approche adoptée et les modèles mis au point ont souvent été empiriques. Comme nous l'avons précisé précédemment, il convient de distinguer deux types de transport solide:

Afin de mettre en évidence l'ensablement et l'érosion autour du récif artificiel dans des conditions très simplifiées, sous l'unique influence de la houle et en négligeant les courants littoraux, nous nous sommes intéressés dans le cadre de cette modélisation au transport solide par charriage, uniquement.

Contrairement au mode de transport des particules en suspension, le transport par charriage fait intervenir des particules plus grosses. Celles-ci se déplacent sur le fond en glissant ou en roulant. Il existent dans la littérature de nombreux modèles de transport solide par charriage. Nous ne présenterons ici que les plus connu et ceux qui sont en relation avec SYSIPHE, le code de calcul que nous aurions voulu utiliser pour la modélisation.

retour
 
 

1/Les modèles déterministes
    Les modèles déterministes donnent un débit solide en fonction des conditions hydrauliques et des caractéristiques géométriques des grains. L'équation de Meyer-Peter (1948) en est un des meilleurs exemples. Cette formulation est utilisée par SISYPHE Il s'agit d'une relation empirique, testée en écoulement permanent et sa forme simplifiée est:
 
 



 






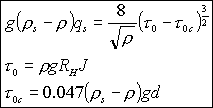
    La formule de Meyer-Peter fait intervenir un cisaillement critique au-dessous duquel le transport solide est nul. Cette idée de seuil nous ne retrouverons pas dans le modèle d'Einstein (brièvement explicité ultérieurement). Les conditions de validité de la relation de Meyer-Peter, portant sur la hauteur d'eau, la pente du fond, le diamètre des grains et la densité des particules sont les suivantes:
 
 



 






Il s'agit, tout de même ici de la forme simplifiée de la formule de Peter-Meyer. Cependant, les explications précédentes nous permettent de comprendre les modèles utilisés par les codes de calcul pour la détermination du transport solide.

retour
 

2/Les modèles statistiques
    Ces modèles sont basés sur une approche probabiliste des phénomènes. Le plus connu est le modèle d'Einstein. Il s'agit d'un des premiers modèles à faire intervenir la turbulence et les distributions de fluctuations en termes stochastiques. En effet, à partir des considérations hydrodynamiques locales, ce modèle permet d'arriver à une approche globale.

Pour l'établissement de ce modèle, les cinq hypothèses suivantes ont été utilisées:

-La mise en mouvement d'une particule par un écoulement dépend de la géométrie de la particule et des conditions locales de l'écoulement.

-Une particule est mise en mouvement une fois que la force de portance exercée sur la particule sous l'action de la houle est supérieure au poids immergéde la particule.

-Une fois la particule en mouvement, la probabilité pour qu'elle s'arrête est la même en tout point de l'écoulement, sauf aux endroits où l'écoulement possède les propriétés nécessaire pour la mise en mouvement de la particule en question.

La distance parcourue par une particule entre deux points d'arrêt est indépendante des conditions hydrauliques de l'écoulement, de l'intensité du transport solide et de la composition du lit. Pour une particule sphérique, cette distance est une fonction linéaire croissante du diamètre.

-Deux paramètres sont définis :

1. Le temps d'échange- temps nécessaire pour une particule érodée d'être remplacée par une autre particule

2. La probabilité d'échange- probabilité pour une particule d'être érodée.

Pour obtenir le débit solide recherché, Einstein a utilisé le raisonnement suivant:

On considère n sections de longueur L ( longueur moyenne des bonds d'une particule, supposée constante), de largeur unité, possédant N grains et situées à l'amont d'une section de référence. Le débit solide est obtenu en considérant le flux des particules traversant la section de référence pendant le temps d'échange. Si Pn est la probabilité qu'une particule ait été érodée n fois pendant le temps d'échange, le transport solide s'écrit:
 
 



 






En exprimant la probabilité pour qu'une particule ait été érodée n fois, en fonction de la probabilité d'échange, prise comme une variable gaussienne, Einstein obtient:
 
 



 






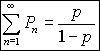
Ce qui conduit à:
 
 



 






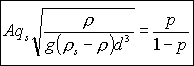
La difficulté de cette formulation réside dans la détermination de la probabilité d'échange. Cependant la prise en compte des structure de turbulence à la paroi peuvent aider à mieux définir les paramètres comme le temps d'échange et la probabilité d'échange.

Avec le modèle d'Einstein on retrouve à peu près les mêmes résultats qu'avec la formule Meyer-Peter, mais sans seuil de débit.
retour
 

Conclusion :

    Comme, malheureusement nous n'avons pas eu le temps de découvrir plus le code de calcul SISYPHE, dans cette partie nous avons expliqué de manière succincte la formulation de la relation simplifiée de Meyer-Peter, utilisée par ce code de calcul. Nous avons voulu aussi, donner une brève explication mathématique des phénomènes de charriage que nous avons décrit en détailles dans les deux parties précédente.
 


Troisième Partie:
B/ Modélisation de la plage de Biscarosse